

When riding a bike, it is good to have steering feedback and a force that pulls the steered wheel back into a centered position.
In normal bikes this centering force is realised by the Caster Effect caused by the pivot angle and the positive trail. This effect is zero when the bike is stopped and it is increasing with the speed.
When trying to build a very low center-steered recumbent one has to face the fact that, with the steering pivot being beneath the seat, one has to implement a very shallow pivot angle to achieve positive trail.
This shallow angle (around 30 deg) has big disadvantages: First the steered front wheel wants to tip into the curve by its own weight (Wheel Flop). A strong steering damper is needed to bring the wheel back to the center. Second the bike is very hard to maneuver because of its huge turning circle.
So what to do? Allowing a negative trail and thus obtaining bigger pivot angles resolves the mentioned problems.
But what about the centering force? The caster effect is gone but another force comes into play now: By turning the wheel, the pivot rises and as the rider sits above the pivot he is also lifted. As the lowest pivot position is the centered wheel, it is pulled back automatically (by gravity) after each steering action.
This Seat Rising Effect is present at any speed and also when the bike is stopped.
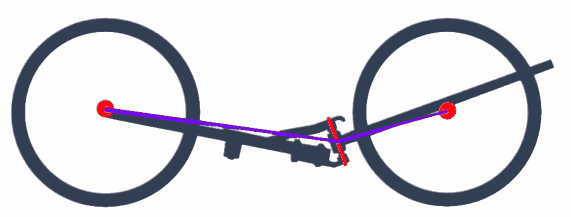
Above there is an illustration of a Python frame. The center pivot and the axles are in red. When a Python bends in the middle, the center pivot rises. For this to happen the rider's weight must be lifted, since he's sitting on top of the pivot.
Which means: The weight of the rider stablilizes the frame by pushing the pivot down. The pivot must be at an angle. If the pivot were vertical (to the ground), then the frame could bend without lifting the weight of the rider, and the Python would be a flip-flop instead of a HPV.
The following animation shows the self centering and wheel flop effect of a python trike, modelled in a physics engine (Newton Game Dynamics):
Dirk Bonné from Danmark has done some calculations to evaluate the maximum seat rising depending on trail and pivot angle. Dirk also developed a free program for everybody to make own experiments with various geometries.
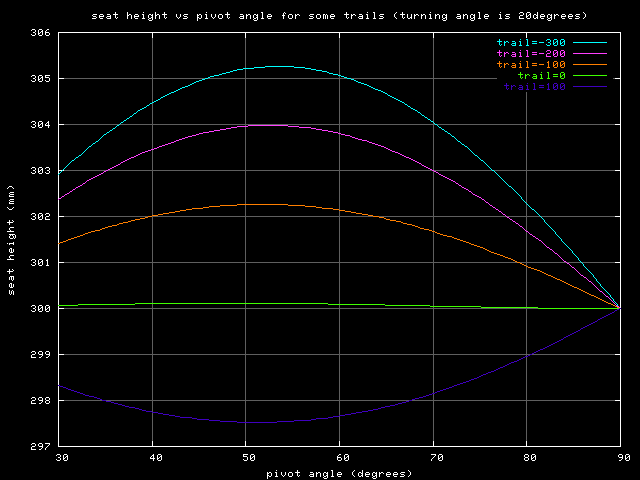
The above graph shows the changing of the seat rising effect against the pivot angle and the trail. The maximal self centering effect is around 53° pivot angle, with trail having only a little influence. When going below that angle the centering capability drops again. The dark blue line with positive trail (flevobike) shows the absence of seat rising.
By looking at the graph one could naively conclude that the best pivot angle is around 53°, because it yields the biggest seat rising effect.
This is true, but there is still the wheel flop which comes into play at shallow angles. I tested the 53° geometry by building an experimental python. Riding behaviour was very bad as the front part constantly kept swinging from one side to the other. So I gradually increased the pivot angle until the bike became rideable at exactly 63°.
This "Sweet Spot" was amazingly sharp bounded at its lower edge (two degrees lower and the bike became unrideable) and diffuse bounded at its upper edge (bigger pivot angles were still rideable, but the self centering effect declined and so did the steering feedback).
Not really, but it is close: The optimal pivot angle is exactly the one where the weight of the whole front part (including the riders legs) is in equilibrium with the rest of the bike (including the rest of the rider). This is different with every bike and rider. To be more exact: It is the angle where the wheel flop effect is overcompensated by the seat rising effect.
The heavier the rear part is in relation to the front, the closer the pivot angle may approach the desired maximum seat rising angle.
For those who want to be on the safe side I recommend a pivot angle of 65°.
